FAQ/ 射流が生じる場合の河川水位の計算¶
射流が生じる場合、射流の河川水位が出力されますか。
河道の勾配が急な区間を含む河川、特にフルード数 Fr が1を上回るような河道区間がある場合、常流と射流が混在した流れが発生すると思います。DioVISTAはこうした流れに対応した計算ができますか。
また、その場合、どのような手法で常射流混在の流れを計算していますか。テクニカルリファレンスでは、河道モデルをリープフロッグ法の風上差分で算定することになっていますが、このような単純な方法で、射流が発達するような区間の計算を安定的に算出できるのでしょうか。何か、特殊な工夫をされているのでしょうか。
回答¶
DioVISTAの不定流(時間変化のある流れ)では、運動方程式を使っており、常流・射流を分けて解いていません。安定な計算を実現するため、いくつか独自の工夫を行っております。私どもはこれらの手法の詳細について公開しておりませんので、詳細については回答を控えさせていただきます。
DioVISTAの不等流(時間変化のない流れ)では、エネルギー保存則を使っており、常流・射流・跳水を分けて解いています。
河川がどの勾配を超えると不安定になるかを検証はしておりませんが、常射流混合の再現性についてまとめた資料がありますので、その一部をお示しします。
1次元不等流解析との比較その1(常流)¶
| 対象水路 | 人工水路 |
| 水路の条件 | 底幅b=6 m、岸の傾斜z=2、勾配S0=0.0016、粗度係数n=0.025の台形断面プリズム水路が流量Q=10 m^3/s を流している。下流端が崖になっている。ただし、エネルギー係数alpha=1.10とする。 |
| 比較対象 | 岡本芳美 開水路の水理学解説 p. 180, 例題4.2 |
| 比較対象の計算条件 | エネルギー保存則を用いた一次元不等流計算(直接逐次法) |
計算結果
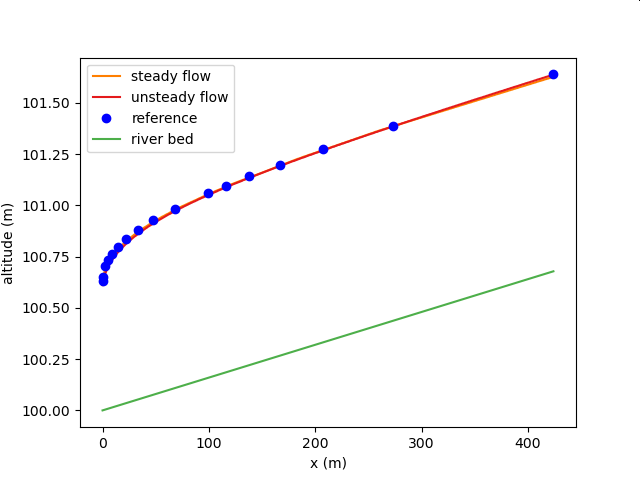
1次元不等流解析との比較その2(常流)¶
| 対象水路 | 人工水路 |
| 水路の条件 | 底幅b=6 m、岸の傾斜z=2、勾配S0=0.0016、粗度係数n=0.025の台形断面プリズム水路が流量Q=10 m^3/s を流している。この水路下流端に広頂堰を設けたら、堰の直上流の水深は1.5 mになった。ただし、エネルギー係数alpha=1.10とする。 |
| 比較対象 | 岡本芳美 開水路の水理学解説 p. 188, 例題4.5 |
| 比較対象の計算条件 | エネルギー保存則を用いた一次元不等流計算(標準逐次法) |
計算結果
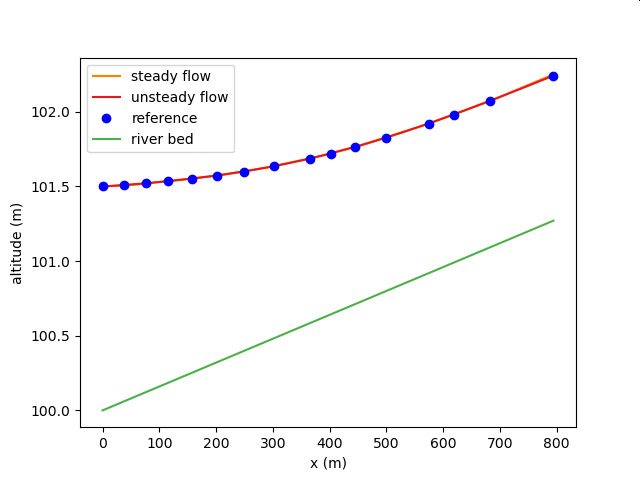
1次元不等流解析との比較その3(常流)¶
| 対象水路 | 人工水路 |
| 水路の条件 | コンクリート製の幅2 m、底勾配1/1000の長方形断面水路がある。これに3.0 m^3/sの流量が流れ、水路の下流端には堰が設けられている。堰直前の水深が1.5 mとする。水路のマニングの粗度係数はn=0.014、エネルギー係数alpha=1.0とする。 |
| 比較対象 | 林泰造 基礎水理学 p. 268, 例題1 |
| 比較対象の計算条件 | エネルギー保存則を用いた一次元不等流計算(直接逐次法) |
計算結果
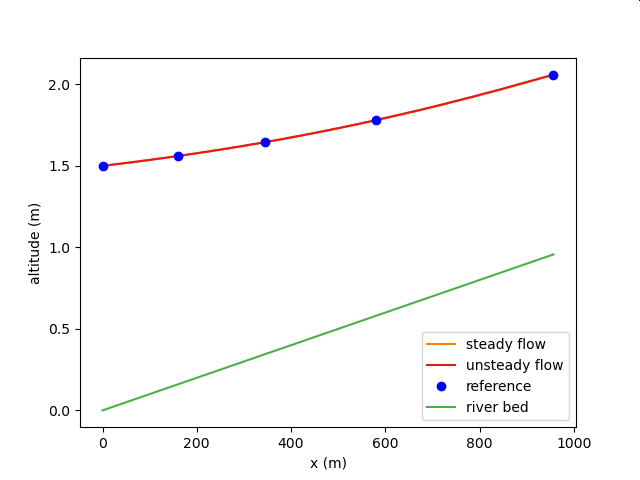
1次元不等流解析との比較その4(常流)¶
| 対象水路 | 人工水路 |
| 水路の条件 | 内法1.6 m×1.6 mの正方形断面を有する長さ70 mの鉄筋コンクリート製暗渠で貯水池から定常的に7 m^3/sの水を放流する。暗渠の勾配は 1/50、マニングの粗度係数はn=0.014、エネルギー係数alpha=1.0とする。 |
| 比較対象 | 林泰造 基礎水理学 p. 271, 例題2 |
| 比較対象の計算条件 | エネルギー保存則を用いた一次元不等流計算(直接逐次法) |
計算結果
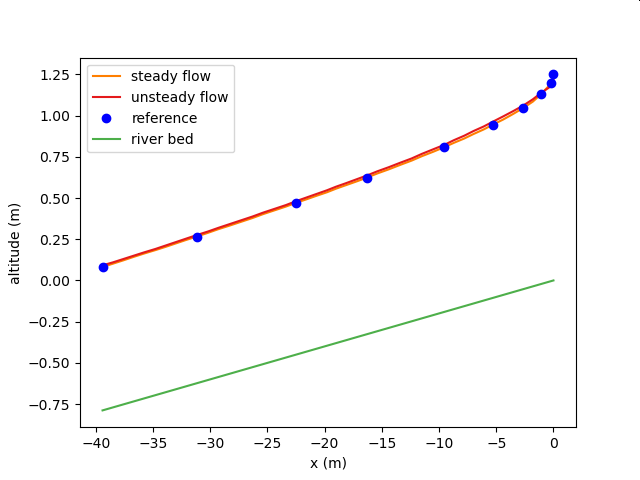
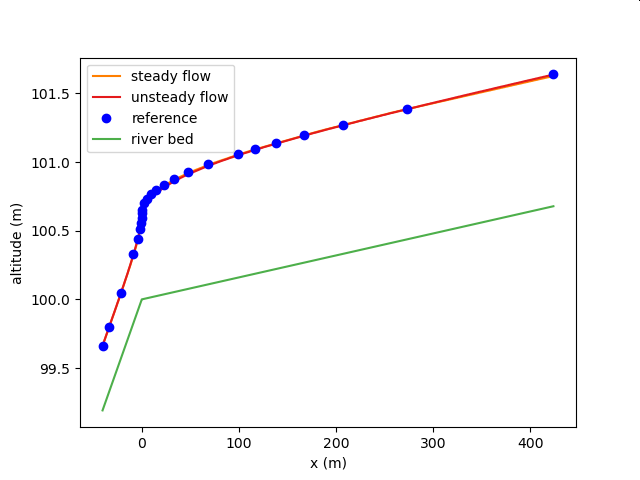
1次元不等流解析との比較その5(常射流混在)¶
| 対象水路 | 人工水路 |
| 水路の条件 | 底幅b=6 m、岸の傾斜z=2、勾配S0=0.0016、粗度係数n=0.025の台形断面プリズム水路が流量Q=10 m^3/s を流している。ある点から折れ曲がって、勾配がS0=0.02に変わる。ただし、エネルギー係数alpha=1.10とする。 |
| 比較対象 | 岡本芳美 開水路の水理学解説 p. 184, 例題4.4 |
| 比較対象の計算条件 | エネルギー保存則を用いた一次元不等流計算(直接逐次法) |
計算結果
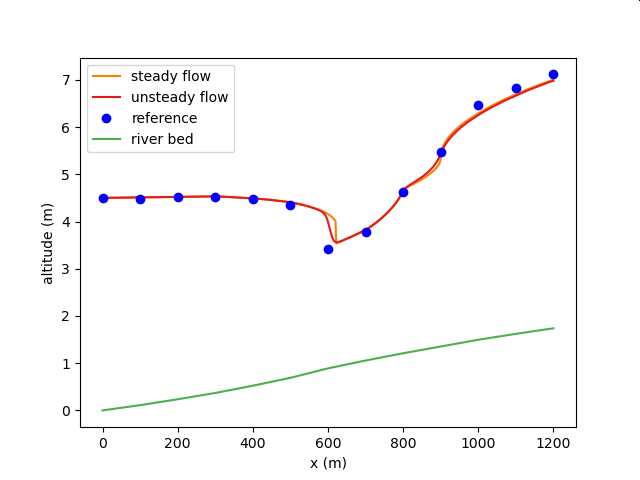
1次元不等流解析との比較その6(常射流混在)¶
| 対象水路 | 人工水路 |
| 水路の条件 | 水路幅が変化する長方形断面河川に流量Q=1,000 m3/s の水が流れる。ただしマニングの粗度係数n=0.025、エネルギー係数alpha=1.1、下流端水位を4.5 mとし、水路幅b、河床勾配、および下流端から12区間の各距離xは下表に示すとおりとする。 |
| 比較対象 | 林泰造 基礎水理学 p. 277, 例題 |
| 比較対象の計算条件 | エネルギー保存則を用いた一次元不等流計算(標準逐次法) |

計算結果
最終更新日:
2022-01-07